CS50 筆記:第三講 Algorithms
筆記前言
本章先簡介了時間複雜度的概念,帶了一點 struct,最後一大半在講不同的 sorting 方式。
Lecture 3 Algorithms
英文講義:https://cs50.harvard.edu/college/2020/fall/notes/3
執行時間
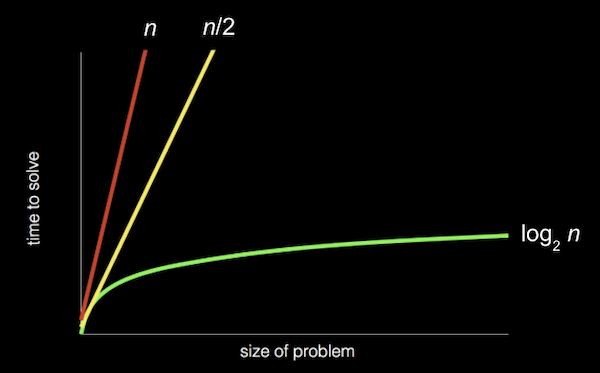
第 0 講的時候介紹了兩種搜尋方式:一頁一頁查找電話簿的 linear search & 把電話簿拆半再拆半的 binary search(其實還有每兩頁找一次的進化版 linear search XD)
這三種方式的執行時間分別是
| 方式 | 時間 |
|---|---|
| 一頁一頁找(linear) | n |
| 兩頁兩頁找 | n/2 |
| 拆半拆半找(二分搜尋) | log2 n |
在估時間複雜度的時候會把常數省略,常數的影響沒有像次方、對數這麼大,例如 n 跟 n/2 跟 3n 都是 n。log2 n 跟 log3 n 都是 log n。
時間複雜度
這裡介紹了兩種 notation, big O 跟 big omega。表示方式像是 O(n)、Ω(n),唸作 big O of n。
big O 在描述這個資料量與執行時間之間的函數的 upper bound,代表執行時間的最壞情況。
big omega 則是 lower bound,代表最佳情況。
| 方式 | O | Ω |
|---|---|---|
| linear search | O(n) | Ω(1) |
| binary search | O(log n) | Ω(1) |
Structs
比方說有聯絡人的資料,比起把聯絡人姓名跟電話分成兩個 array 存,把它用 struct 組織起來操作也比較不容易出錯。
bad
string names[] = {"Brian", "David"};
string numbers[] = {"+1-617-495-1000", "+1-949-468-2750"};
good
typedef struct
{
string name;
string number;
}
person;
// inside main function
person people[2];
people[0].name = "Brian";
people[0].number = "+1-617-495-1000";
people[1].name = "David";
people[1].number = "+1-949-468-2750";
排序
之所以能夠用 binary search 有一大前題是,要找資料的那個 array 資料是有 sort 過的。
電腦無法像人類一樣一眼望過去就知道怎麼排序移動,只能一次查看一個 item、一次調動一個 item。
selection sort
助教影片:https://video.cs50.io/3hH8kTHFw2A (看數字動一次勝過千言萬語啊)
從最左邊開始選定一個數字,把他跟目前右手邊最小的數字交換。
bubble sort
助教影片:https://video.cs50.io/RT-hUXUWQ2I 兩個兩個做比對,當左邊的元素比右邊大,就左右邊的互換。
merge sort (top-down)
助教影片:https://video.cs50.io/Ns7tGNbtvV4 把整個 array 切成一個個小 array。切到只有一個元素的時候,每個只有 1 個元素的 array 都是排好的。接著再把排好的 array 接在一起。因為元素已經排序過,所以可以只比較最左(最小)的元素。
Lab 3
題目給了三支程式 sort1, sort2, sort3,還有一些排序方式不同的資料。要判斷這三個 sort 的程式分別是用哪一種方式(selection? bubble? merge?)來實作。
簡單地寫一下我的解答:
底下是我拿去執行 50000 筆資料的秒數。
| 資料/哪一支程式 | sort1 | sort2 | sort3 |
|---|---|---|---|
| sorted | 4 | 1 | 8 |
| random | 16 | 3 | 6 |
| reversed | 12 | 3 | 8 |
sort2 穩定地時間很短,應該是 nlogn 的 merge sort
sort1 「已排序」跟「沒有排」的資料執行時間差很多,應該是交換排序(最佳情況 n, 平常 n^2)
所以 sort3 應該是 selection sort。
練習寫 merge sort
先寫了 ruby 版的,但覺得 ruby 拿來寫這個很沒 fu XD(執行時間就素慢(誤
def merge_sort(numbers)
return numbers if numbers.length <= 1
left_half, right_half = split_sort(numbers)
return merge_array(merge_sort(left_half), merge_sort(right_half))
end
def split_sort(numbers)
length = numbers.length
raise 'There should be more than 2 elements in the array' if length < 2
left_half = numbers[0 .. (length / 2 - 1)]
right_half = numbers[length / 2 .. length]
return [left_half, right_half]
end
def merge_array(arr1, arr2)
result = []
while true
# 其中一個 array shift 空了就把還剩下的往 result 後面接
return result + arr1 + arr2 if arr1.empty? || arr2.empty?
next result.push(arr1.shift) if arr1.first < arr2.first
result.push(arr2.shift)
end
end
merge_sort([10, 5, 13, 4, 1, 11, 3, 12, 8, 9, 6, 2, 7])
接著挑戰寫一下 C。對 C 的操作還不太熟(苦笑),先直接更動了原 array。
#include <stdio.h>
#define NELEMS(x) (sizeof(x) / sizeof((x)[0]))
void merge_sort();
void merge_array();
int main(void) {
int num[] = {10, 5, 13, 4, 1, 11, 3, 12, 8, 9, 6, 2, 7};
merge_sort(num, 0, NELEMS(num) - 1);
printf("Result: ");
for (int i = 0; i < NELEMS(num); ++i){
if(i != 0)
printf(", ");
printf("%d", num[i]);
}
printf("\n");
}
void merge_sort(int num[], int idx, int last_idx) {
if(idx >= last_idx)
return;
int mid_idx = (idx + last_idx) / 2 + 1;
merge_sort(num, idx, mid_idx - 1);
merge_sort(num, mid_idx, last_idx);
merge_array(num, idx, mid_idx, last_idx);
}
void merge_array(int num[], int idx, int mid_idx, int last_idx){
int length = last_idx - idx + 1;
int ori_mid_idx = mid_idx - idx;
int ori_num[length];
int lselect = 0;
int rselect = ori_mid_idx;
// 把 num array 複製進 ori_num
for(int i=0;i<length;i++){
ori_num[i] = num[idx + i];
}
// ori_num 是原本 left 跟 right 的內容
// 判斷完誰大誰小以後直接更動原 array
for(int j=0;j<length;j++){
if (rselect >= length){
num[idx + j] = ori_num[lselect++];
} else if (lselect >= ori_mid_idx){
num[idx + j] = ori_num[rselect++];
} else if (ori_num[lselect] < ori_num[rselect]){
num[idx + j] = ori_num[lselect++];
} else {
num[idx + j] = ori_num[rselect++];
}
}
}